BS模子 又称什么
BS模子 ,全称为Black-Scholes模子 ,是金融衍生品订价 范畴 中的一项革命性理论,由Fisher Black和Myron Scholes于1973年提出,Robert Merton也对其举行 了紧张 贡献,因此该模子 也被称为Black-Scholes-Merton模子 。这一模子 重要 用于欧式期权的订价 ,是当代 金融理论中的一个紧张 里程碑。
BS模子 的核心 头脑 是基于以下几个假设:市场是有效 的,股票代价 依照 多少 布朗活动 ,颠簸 率恒定,无风险利率已知且恒定,市场不存在买卖 业务 本钱 和税收,且答应 连续 买卖 业务 。在这些假设的底子 上,BS模子 通过数学公式盘算 出期权的代价 。
BS模子 的公式如下:

C = S * N(d1) - X * e^(-rT) * N(d2)
P = X * e^(-rT) * N(-d2) - S * N(-d1)
此中 ,C表现 看涨期权的代价 ,P表现 看跌期权的代价 ,S是标的资产的当前代价 ,X是期权的实行 代价 ,r是无风险利率,T是期权到期时间,N(x)是标准 正态分布的累积分布函数,d1和d2是根据公式盘算 出的中心 变量。
BS模子 的提出,不但 为期权订价 提供了一个科学的框架,也极大地推动了金融衍生品市场的发展。然而,实际 应用中,BS模子 的假设条件每每 难以完全满意 ,因此在实际 操纵 中必要 根据市场环境 举行 得当 的调解 和修正。
以下是一个简单 的表格,展示了BS模子 中各个参数的寄义 及其在模子 中的作用:
参数 寄义 在模子 中的作用 S 标的资产的当前代价 直接影响期权的代价 X 期权的实行 代价 决定期权的内涵 代价 r 无风险利率 影响期权的时间代价 T 期权到期时间 影响期权的时间代价 N(x) 标准 正态分布的累积分布函数 用于盘算 期权代价 的概率因素BS模子 的应用广泛,不但 在期权订价 中,也在风险管理、资产设置 等范畴 发挥着紧张 作用。明白 和把握 BS模子 ,对于期货买卖 业务 者来说,是提拔 买卖 业务 技能和风险控制本领 的关键。
相关文章
猜你喜欢
-
算力服务管理成“香饽饽” 慧辰股份发布融合算力管理服务平台
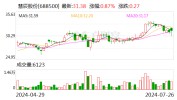
依托数据分析、数据发掘和数据运业务务底子,慧辰股份(维权)开始在智算与AI应用服务范畴布局提速。7月26日,公司发布自研智算服务体系化产物方案,包罗“融合算力管理服务平台”和“慧AI”两款产物。慧辰股份CTO马亮博士告诉记者,不完全统计,近两年在建智算项目有数百家。对于大量...
-
美股市场大幅抛售,“恐惊 指数”创下三个月新高

专题:科技巨头财报不佳引发恐慌抛售美股暴跌 周三,美股的大幅抛售使华尔街最受关注的市场颠簸率指标创下三个月新高,并提振了期权买卖业务量,只管战略师们险些没有看到恐慌的迹象。 特斯拉和Alphabet财报业绩不佳后,促使投资者质疑由大型科技公司和人工智能推动的2024年反...
-
Meta最强大模子 逾越 GPT-4o,扎克伯格再次挑起开闭源之争

界面消息记者|伍洋宇界面消息编辑|宋佳楠 继OpenAI忽然上线一款“小模子”GPT-4omini之后,Meta决定抛出其超大参数的大模子炸场。 7月24日,Meta发布了开源大模子系列Llama3.1405B,以及升级后的70B和8B两个尺寸模子。 Ll...
-
科技股财报季到临对冲科技巨头下跌风险的看跌期权受到追捧

专题:聚焦美股2024年第二季度财报 科技巨头本年驱动了美国股市大幅上涨,但买卖业务员如今正在预备欢迎诸如英伟达等公司股票的潜伏下跌,由于有担心以为该板块涨得过快过猛。 根据市场数据和战略师的说法,买卖业务员正在买入防范英伟达和其他大型科技股以及纳斯达克100指...
-
中国信通院正式启动AI大模子 算子适配生态建立 工作

快讯择要【中国信通院正式启动AI大模子算子适配生态建立工作】证券时报e公司讯,据中国信通院CAICT微信公众号,为加快大模子软硬件协同生态构建,推动差别尺寸、范例模子与芯片软件栈、Trito...
最新发布
-
200多家公司脱手港股年内回购逾1500亿港元
2024-07-31 -
南山团体 发起部分要约收购 连续看好恒通股份将来 发展
2024-07-31 -
万科拟向苏州高新地产出售合资公司50%股权
2024-07-31 -
小摩下调诺瓦瓦克斯医药评级至“减持”
2024-07-31 -
“白酒股下跌空间已不大!”公募人士不认同瑞银证券看空观点 多家酒企也回应了
2024-07-31
